Currently available Master’s thesis projects
Below is a list of example projects and topics that we have available for MSc theses. Regardless of your experience with medical imaging, we are confident you will find something that resonates. If you have a specific topic in mind besides the ones listed below, please get in touch with us. Back to Research →
MSc thesis project – in collaboration with the Neuromuscular Center
Advanced imaging of neuromuscular diseases with MRI
Background: MRI can be used to detect nerve lesions, demyelination, or axonal damage, as well as monitoring muscle degeneration, inflammation, and fat infiltration. Traditional MRI methods rely heavily on qualitative assessments, whereas quantitative MRI offers a more objective approach by quantifying tissue properties directly. However, current MRI techniques are slow, may be sensitive to motion and magnetic field inhomogeneities, and may not capture all necessary information to visualize and discern healthy from diseased tissue.
Aim: To develop and validate an MRI approach that provides enhanced visualization of nerve lesions and quantitative imaging of skeletal muscle, ensuring faster acquisition and improved diagnostic accuracy. This will provide new insights into neuromuscular diseases.
Project: This is a joint project between our group (Prof. Bastiaansen) and the Neuromuscular Center (PD Dr. Med Olivier Scheidegger). Building on recent work in brain, liver, and cartilage imaging, the MRI sequence will be adapted for optimal nerve and muscle contrast. To maintain quantitative accuracy at high resolution, acceleration strategies will be applied. Data will be processed using established pipelines for T1, T2, and fat fraction quantification, and compared to standard clinical protocols. AI-based segmentation will ensure consistent anatomical differentiation. The method will be validated in phantoms, healthy volunteers, and patients with neuromuscular diseases.
MSc thesis project – in collaboration with CSEM
Next-generation biomarker quantification in the human brain with innovative MRI techniques at ultra-high magnetic field.
Background: Human brain imaging with MRI is critical to quantify brain function and biomarkers of disease. Despite the improvements in signal and spatial image resolution that MRI at high field (7T) offers, the imaging technique is limited by hardware constraints, which restricts the amount of biomarkers that can be quantified. The project lies at the interface of medicine, physics, and engineering to develop novel imaging tools for clinical use.
Aim: The aim of this MSc thesis is to develop a new method to enable the simultaneous quantification of magnetic susceptibility (QSM) and relaxation times (T1, T2) in the human brain at 7T, which is currently not possible.
Project: This is a joint project between our group (Prof. Bastiaansen) and CSEM (Dr. Jorge) to develop and optimize a novel post-processing framework to convert MRI signals into quantitative parameters of brain disease. You will participate in MRI scans to optimize data acquisition strategies. Initially, different post-processing tools will be tried and compared. You will investigate the correlation between different acquisition strategies and signal processing methods to optimize for both MRI biomarker quantification (T1, T2, magnetic susceptibility) and scan time. The final step will include the comparison with state-of-the art approaches.
MSc thesis project – in collaboration with SCAN
Quantification of brain microstructure dynamics using MRI
Background: Microstructural information is crucial for early disease detection at the cellular level. Diffusion-weighted imaging (DWI) using MRI is capable of extracting microstructural details by measuring MRI signal changes caused by Brownian motion. While pre-clinical MRI methods based on non-oscillating gradient spin-echo (NOGSE) sequences allow the detailed observation of microstructural sizes, these methods are inaccessible on clinical scanners, due to hardware limitations, long measurement times or high gradient demands, restricting clinical use.
Aim: The aim of this MSc thesis is to participate in the development of a novel diffusion MRI technique (NOGSE sequence) for use in clinical scanners, maintaining sensitivity with clinically feasible control parameters.
Project: This is a collaborative project with the Support Center for Advanced Neuroimaging (Dr. Milena Capiglioni) and the Department of Medical Physics at the Balseiro Institute in Argentina. We aim to develop and optimize the NOGSE approach to overcome clinical hardware limitations. You will participate in MRI scans to refine data acquisition strategies. Initially, we will establish the limits of control parameters, such as maximum gradient strength (G) and diffusion time (TN). Data will be acquired from yeast phantoms, and diffusion models will be used to determine which diffusion regimes are accessible with a 3T clinical scanner. You will study and optimize acquisition parameters to enhance sensitivity. The final step will involve comparing NOGSE with state-of-the-art diffusion sequences.
MSc thesis project
Enabling Direct imaging of Neuronal Activity with MRI
Background: Direct imaging of neuronal activity is challenged by insufficient sensitivity and spatial accuracy. Novel MRI methods, such as Spin-lock based functional MRI, target the oscillatory magnetic fields in the brain induced by neuronal activity. These fields can be detected at specific frequencies, making it possible to target frequencies associated with pathological neuronal activity (e.g. epilepsy). We have demonstrated a high sensitivity and reproducibility of the method in phantoms, but the translation to the human setting requires faster data sampling strategies.
Aim: The goal of this project is to compare and evaluate the performance of different data sampling strategies based on the physical properties of the Spin-lock based MRI signal.
Project: This is a collaborative project with the Support Center for Advanced Neuroimaging (Dr. Milena Capiglioni). Using the Pulseq framework, the student will implement the Spin-lock preparation on different readout options accessible on the Pulseq platform. The project involves: 1) Implementing and testing various data sampling methods on a 3T MRI scanner. 2) Conducting a comparative analysis against previously tested echo-planar imaging (EPI) to evaluate sensitivity and readout artifacts. 3) Performing experiments on an electrical phantom that mimics neuronal behavior. 4) Analyzing available post-processing techniques and including them in the comparison.
The expected outcome is a proposed pipeline for direct imaging of neuronal activity, encompassing both acquisition and analysis methods.
MSc thesis project:
Revolutionizing the assessment of cardiac function with cutting-edge Cine MRI techniques
Background: Cardiac cine MRI is a vital tool in routine clinical cardiac exams that helps to assess the function of the heart. Despite its tremendous potential this imaging technique is typically corrupted by artifacts that limit its reliability and accuracy.
Aim: The aim of this MSc thesis is to develop a new method for image artifact removal in cardiac cine MRI that enables more accurate cardiac function assessment.
Project: As part of this project, you will work with our team to develop a novel cardiac cine MRI technique in our lab. You will participate in MRI data acquisition and post-processing. You will work on extracting physiological signals to sort the data into different cardiac time frames and you will use and learn about novel algorithmic tools to remove image artifacts in cine MRI. The next step will be to use the measured data to quantify clinical parameters assessing the cardiac function, such as the ejection fraction, and to compare the results to other state-of-the-art approaches.
MSc thesis project:
Novel methods for white and grey matter-specific biomarker quantification at 3T and 7T
Background: Recent advances in quantitative MRI are uniquely suited to obtain a variety of biomarkers that could be relevant for assessing brain function and disease. To validate new methods, it is essential to accurately depict different brain regions in which biomarkers can be attributed. Nevertheless, existing methods for brain region segmentation are, as of yet, incompatible with novel quantitative MRI methods. The project lies at the interface of medicine, physics, and engineering to develop novel imaging tools for clinical use.
Aim: The aim of this MSc thesis is to translate and implement segmentation methods to be used with in-house developed MRI technology to quantify biomarker properties specifically in white and grey matter.
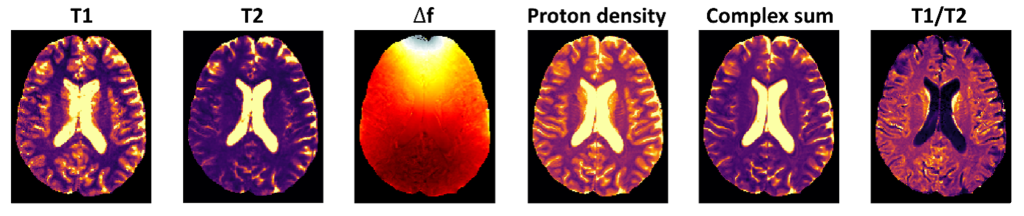
Project: You will initially perform brain segmentations for white and grey matter based on existing techniques developed for T1-weighted (MP2Rage) MRI data. The obtained segmentations will be used to validate the white and grey matter-specific quantitative maps (T1, T2, PD) obtained with novel quantitative MRI methods and state-of-the-art approaches. In addition, it will be tested whether proton density (PD) maps can be a substitute for conventional T1 weighted images for brain segmentations.
MSc thesis project:
The influence of fat signal suppression on biomarker quantification with MRI
Background: Quantitative MRI is performed in clinical routine to determine tissue structure and function noninvasively. Despite its tremendous potential, conventional quantitative MRI methods are sensitive to multicompartment effects, such as the presence of different tissue types (such as fat) within a single imaging voxel. There is a knowledge gap in how to untangle or suppress unwanted fat signal sources to perform robust biomarker quantification with MRI.
Aim: The aim of this MSc thesis is to test a new method that suppresses unwanted fat signals, and to determine the benefits and limitations of its use in quantitative MRI.
Project: As part of this project, you will work with our team to test a novel fat suppression method that was developed in our lab. The influence on biomarker quantification will be tested first by numerical simulations. Simulations will be performed to evaluate the effect of different tissue frequency distributions on T1 and T2 estimation using a novel acquisition method developed in our lab. MRI experiments will then be performed in dedicated standardized phantoms in our lab, and finally in a human volunteer. Therefore, you will participate in MRI data acquisition and post-processing.
MSc thesis project:
Implementing and evaluating a vendor-independent 3D-radial sequence in an open-source framework
Background: The surge in cardiac MR imaging for patients with implantable cardioverter-defibrillators (ICDs) has accentuated the challenge of ICD artifacts, particularly in the quantification of T1 and T2 maps, critical for accurate diagnosis and patient care. This population often grapples with the inability to sustain breath holds and is prone to arrhythmias. New technology for simultaneous T1 and T2 quantifications, proves beneficial where susceptibility effects and field inhomogeneity affect MR image quality. However, vendor-specific MRI sequence programming contributes to delays in technical development and collaboration. Hence, there is a pressing need for vendor-independent sequence programming to generate generic sequence files that can be used to acquire comprehensive cardiac images on every scanner.
Aim: The primary objective of this project is to compare the effect that magnetic field distortions have on different MRI data sampling strategies with the aim to decide which strategy mitigates best the debilitating loss in quantitative image quality near metallic implants. Therefore, different MRI methods will be implemented and the resulting qualitative and quantitative images compared.
Project: Using the Pypulseq framework, initially a Cartesian imaging sequence will be implemented by the student and compared against a gold-standard methods implemented in the vendor provided programming environment. Subsequently, a radial acquisition will be programmed in Pypulseq , and a comparative analysis will be conducted against the previously tested Cartesian sequence and against a reference sequence. All experiments will be carried out on a 1.5T, 3T, and 7T MRI scanner using a phantom model and a comprehensive analysis will be performed.
MSc thesis project:
Building a neural network for accurate quantitative MRI maps
Topic: Neural networks, AI, deep learning, MRI data acquisition, signal processing, image reconstruction
Who: Students with a background in computer science, electrical or bio(medical) engineering who are interested in the development of novel imaging applications that are directly translatable to the clinic.

Background: Parameter quantification from a complex MR signal profile under specific excitation schemes such as phase-cycled bSSFP has tremendous potential. Our current signal extraction models rely on signal matching using dictionaries, which became popular with the emergence of magnetic resonance fingerprinting (MRF) approaches. While the dictionary fitting methods are well suited for joint solutions, deep learning-based methods enjoy high inference speed and accuracy. In order to exploit both strengths, we are developing a deep learning method for the complex bSSFP signal profile to enable parameter mapping with the exploitation of joint information.
Project: The prospective student will work with training data from the literature and MRI studies, inspired by MRI physics, build the proposed learning architecture and training it, and assess the finesse of the final product by employing simulation studies and in vitro experiments.
MSc thesis project:
Mathematical modeling in MRI for multi-parameter estimation
Topic: Mathematical modelling, group theory, MRI multi-parameter estimation, simulations, data processing and analysis, complex systems.
Who: Students with a background in mathematics, physics, electrical or bio(medical) engineering. Everyone who is interested in creative mathematical modelling, simulations and parameter estimation on real experimental data.
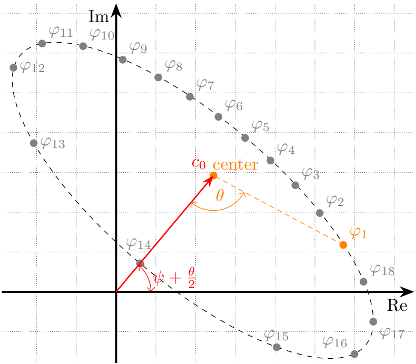
Background: Mathematical models are essential for parameter estimation in quantitative MRI. The dynamics of complex MRI systems are based on different combinations of physical equations. Each physical equation by itself is well understood, but in complex combinations there are different possibilities for parameter estimation. The challenge is to find representations and theory frames which include the whole information about the complex system, while exhibiting lowest possible complexity for the highest possible model-robustness, i.e. irreducible representations, “occam’s razor”-principle. Often a system can be simplified by transforming the mathematical problem into a suitable representation e.g. polar coordinates, complex space, Fourier space or exploiting characterizable invariants of the system, group theory or other algebras. In finding those representations creativity, mathematical knowledge, and physical understanding of MRI is necessary.
Project: In this project, the prospective student will extend or design mathematical models for parameter (T1, T2, water, fat) quantification using MRI signals extracted from phase cycled balanced steady state free precession (bSSFP) data. Instead of using conventional complex space representations, the student will investigate how the robustness of parameter estimation changes using representations such as quaternions and group theoretical approaches, which are not well understood. The model-robustness will be evaluated in simulations (Bloch-Simulations) as well as on experimental data.
MSc thesis project:
Solving MRI inversion problems for robust quantitative parameter extraction
Topic: Inversion problem, regularization, bSSFP, simulations, data processing and analysis, complex systems.
Who: Students with a background in mathematics, computer science, physics, electrical or bio(medical) engineering. Everyone who is interested in new and creative mathematical models and solutions, regularization, computer simulations and parameter estimation on real experimental data.
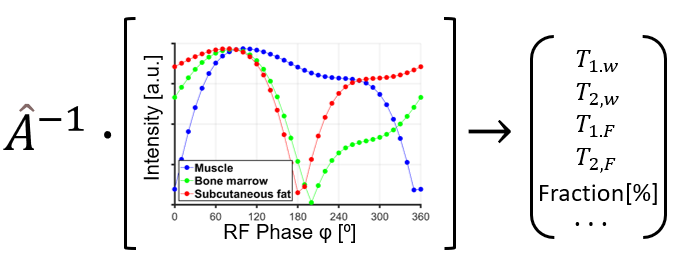
Background: In quantitative MRI the dynamic of a complex physical system is described by the combination of a set of physical equations leading to a certain kind of quantitative model or quantitative map. Those respective models/maps are used for the quantification of e.g. water-fat fractions or T1- and T2-time. By trying to map acquired/simulated data to the quantitative parameter of interest, inversion problems are frequently encountered. Depending on the problem, inversions can be challenging to solve. The challenge can either originate on the sparsity of acquired data or also on the mathematical model itself. The quantification of multi-compartment systems in MRI exhibits a lot of inversion operations, where some problems arise as ambiguities or so called “ill-posed problems”. Sometimes it is possible to find solutions of the inversion by constraining the system to boundary conditions, by reducing the complexity or dimensionality of the model or bring it in another mathematical formulation. Some of those problems are not well understood yet and their solution is key for a robust quantification of multi-compartment systems in MRI.
Project: In this project, it is aimed to first identify a system with known dynamics, and then device a solution technique. In particular, the prospective student will investigate inversion problems that are typical for parameter quantification in multi-compartment systems, like water and fat, with special focus on the bSSFP-sequence. The student will investigate whether a problem can be solved analytically/numerically by an unambiguous mathematical representation or develop a regularized inverse problem-solving technique. Solutions will be tested in simulations and on real experimental data.
